Purpose
Return value
Syntax
=CSC(number)
- number - The angle provided in radians.
Using the CSC function
The CSC function returns the cosecant of an angle provided in radians. In geometric terms, the cosecant of an angle is equal to the ratio of a right triangle’s hypotenuse divided by its opposite side. For example, the cosecant of PI()/6 or 30° returns the ratio 2.0.
=CSC(PI()/6) // Returns 2.0
Using Degrees
The CSC function expects radians. To supply an angle to CSC in degrees, multiply the angle by PI()/180 or use the RADIANS function to convert to radians. For example, to get the CSC of 60 degrees, you can use either formula below:
=CSC(60*PI()/180)
=CSC(RADIANS(60))
Explanation

The graph of cosecant, shown above, visualizes the output of the function for angles from 0 to a full rotation. The function has vertical asymptotes within the range [0, 2π] at the points 0, π and 2π where the output diverges to infinity. CSC is the inverse of SIN and can be equivalently defined in the formula below:
=CSC(angle)=1/SIN(angle)
The relationship between cosecant and sine is visualized by the graph of the two functions shown below:
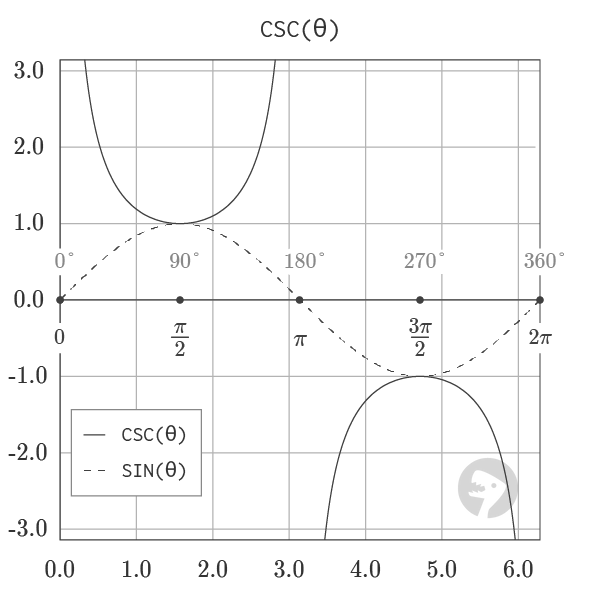
Graphs courtesy of wumbo.net .
Purpose
Return value
Syntax
=CSCH(number)
- number - The hyperbolic angle.
Using the CSCH function
The Excel CSCH function returns the hyperbolic cosecant of an angle. Given the hyperbolic angle of 1, the function returns 0.850918128 as output.
=CSCH(1) // returns 0.850918128
Explanation
The hyperbolic cosecant function is the reciprocal of the hyperbolic sine function.
=1/SINH(a) // equivalent to CSCH(a)