Purpose
Return value
Syntax
=EVEN(number)
- number - The number to round up to an even integer.
Using the EVEN function
The EVEN function rounds numbers up to the next even integer. EVEN always rounds numbers away from zero, so positive numbers become larger and negative numbers become smaller (i.e. more negative).
EVEN takes just one argument, number , which should be a numeric value. With positive numbers, EVEN rounds number up to the next even integer. With negative values, EVEN rounds number down away from zero to the next negative integer. With zero (0) and numbers that are already even integers, number is unchanged.
Examples
The EVEN function rounds positive numbers up to the next even integer:
=EVEN(1) // returns 2
=EVEN(3.1) // returns 4
Negative numbers are rounded away from zero to the next even integer:
=EVEN(-1) // returns -2
=EVEN(-3.1) // returns -4
Zero and numbers that are already even integers are unaffected:
=EVEN(2) // returns 2
=EVEN(0) // returns 0
=EVEN(-2) // returns -2
To round numbers up to the next odd integer, see the ODD function .
Purpose
Return value
Syntax
=EXP(number)
- number - The power that e is raised to.
Using the EXP function
The EXP function finds the value of the constant e raised to a given number, so you can think of the EXP function as e ^(number), where e ≈ 2.718. The exponential function can be used to get the value of e by passing the number 1 as the argument.
=EXP(0) // returns 1
=EXP(1) // returns 2.71828182846 (the value of e)
=EXP(2) // returns 7.38905609893
The exponential function models exponential growth and has the unique property where the output of the function at a given point is proportional to the rate of change of the function at that point. The inverse of the exponential function is the natural logarithm which represents the opposite of exponential growth, exponential decay.
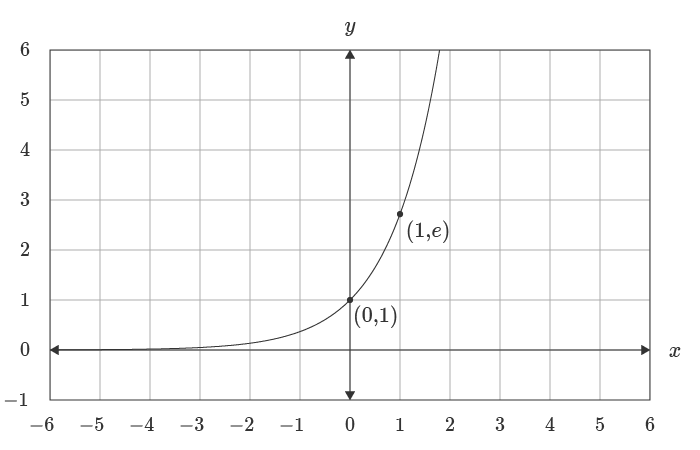
For a more detailed explanation see wumbo.net .
Notes
- e stands for Euler’s number.
- The number e is a famous irrational number, and one of the most important numbers in mathematics.
- The first digits of e are: 2.718281828459…
- e is the base of the Natural Logarithms, invented by John Napier.