Purpose
Return value
Syntax
=GAMMA.INV(probability,alpha,beta)
- probability - The probability associated with the gamma distribution (must be between 0 and 1).
- alpha - The shape parameter of the distribution.
- beta - The scale parameter of the distribution.
Using the GAMMA.INV function
GAMMA.INV is used to find the value at which the cumulative gamma distribution reaches a specified probability. In other words, it answers the question: “For a given probability, what is the corresponding value of x in the gamma distribution?” This is also known as the quantile or percentile function.
Key features
- Returns the value of x for a given cumulative probability
- Useful for calculating percentiles, thresholds, or cutoffs
- Shape parameter (alpha) controls the distribution’s shape
- Scale parameter (beta) controls the distribution’s spread
- Requires all parameters to be positive numbers
- Inverse of the GAMMA.DIST function with cumulative = TRUE
GAMMA.INV is the updated version of GAMMAINV . While GAMMAINV is still available for backward compatibility, Microsoft recommends using GAMMA.INV for new work as it provides better accuracy.
- Key features
- Example #1 - Find a waiting time threshold
- Example #2 - Relationship to GAMMA.DIST
- Example #3 - Calculate value at percentile
- How GAMMA.INV is approximated
- Related functions
- Notes
Example #1 - Find a waiting time threshold
Suppose you work at a stall at the farmers’ market. Customers appear one at a time, at random, but historical data tell you they arrive on average 10 per hour . You want to know the maximum time you would have to wait for the 20th customer to show up, such that there is a 90% chance the 20th customer will have arrived by that time.
To set up the problem as a gamma distribution:
- Rate (λ): 10 customers per hour
- Shape parameter (alpha): 20 (the number of customers we’re waiting for)
- Scale parameter (beta): 1/λ = 0.1 hours per customer
- Probability: 0.9 (90% chance)
To find the time by which there is a 90% chance the 20th customer will have arrived:
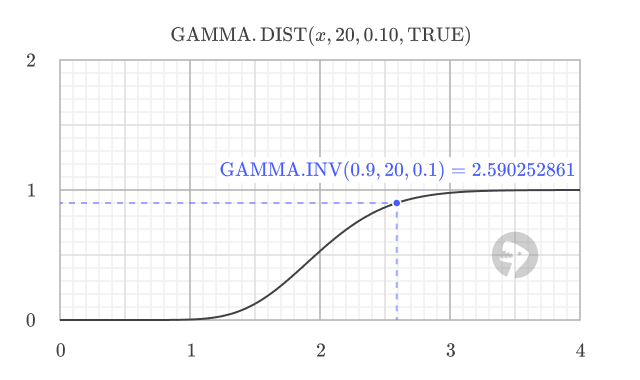
=GAMMA.INV(0.9, 20, 0.1) // returns 2.590252861
This means there is a 90% chance that the 20th customer will arrive within 2.59 hours.
Example #2 - Relationship to GAMMA.DIST
GAMMA.INV is the inverse of GAMMA.DIST with cumulative = TRUE. For example, using the result from above, you can check the probability of the 20th customer arriving within 2.59 hours with:
=GAMMA.DIST(2.590252861, 20, 0.1, TRUE) // returns 0.9
In other words, GAMMA.INV finds the value for a given probability, and GAMMA.DIST with cumulative = TRUE finds the probability for a given value. Below is a graph of the gamma distribution CDF with the point where the probability is 0.9 showing the inverse relationship.
Example #3 - Calculate value at percentile
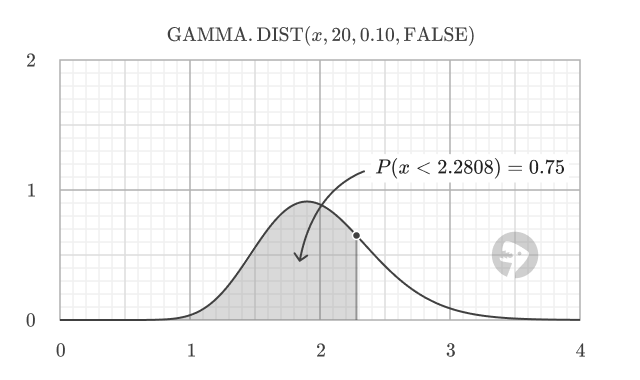
In general, you can use GAMMA.INV to find the value at the percentile of a gamma distribution. For example, to find the value at the 25th, 50th, and 75th percentiles for a gamma distribution with alpha = 20 and beta = 0.1
=GAMMA.INV(0.25, 20, 0.1) // returns 1.683014746
=GAMMA.INV(0.50, 20, 0.1) // returns 1.966767242
=GAMMA.INV(0.75, 20, 0.1) // returns 2.280800681
The percentile corresponds to the area under the probability density function (PDF) to the left of a specific threshold value. For example, the 75th percentile is the value at which 75% of the distribution lies to the left, representing a cumulative probability of 0.75.
How GAMMA.INV is approximated
According to Microsoft, GAMMA.INV is calculated using an iterative search technique. Given a probability, GAMMA.INV seeks the value x such that GAMMA.DIST(x, alpha, beta, TRUE) equals the specified probability. The precision of GAMMA.INV depends on the precision of the GAMMA.DIST function. If the search does not converge after 64 iterations, GAMMA.INV returns the #N/A error value.
Related functions
Excel offers several related functions for working with the gamma and other distributions:
- GAMMA.DIST - Calculate gamma distribution values (PDF or CDF)
- GAMMALN - Calculate natural logarithm of gamma function
- WEIBULL.DIST - Calculate Weibull distribution (related to gamma)
- EXP.DIST - Calculate exponential distribution (special case of gamma)
- CHISQ.INV - Inverse of the chi-squared distribution (special case of gamma)
Notes
- All parameters (probability, alpha, beta) must be positive numbers
- Probability must be between 0 and 1 (exclusive)
- If probability < 0 or ≥ 1, the function returns #NUM! error
- If alpha ≤ 0 or beta ≤ 0, the function returns #NUM! error
- If any argument is non-numeric, the function returns a #VALUE! error
- GAMMA.INV provides improved accuracy over the legacy GAMMAINV function
Purpose
Return value
Syntax
=GAMMADIST(x,alpha,beta,cumulative)
- x - The value at which to evaluate the distribution.
- alpha - The shape parameter of the distribution.
- beta - The scale parameter of the distribution.
- cumulative - A logical value that determines the form of the function. If TRUE, returns the cumulative distribution function; if FALSE, returns the probability density function.
Using the GAMMADIST function
The GAMMADIST function calculates values for the gamma distribution, which is a continuous probability distribution commonly used in statistical analysis. The gamma distribution is particularly useful for modeling positive continuous variables and has applications in reliability analysis, queuing theory, and meteorology.
For better accuracy and consistency with other modern statistical functions, it is recommended to use the GAMMA.DIST function . GAMMA.DIST uses the same arguments and provides the same core functionality with improved numerical precision. See the GAMMA.DIST function for more details.
Notes
- GAMMADIST is a legacy function. For Excel 2010 and later, use the GAMMA.DIST function.
- If any argument is non-numeric, GAMMADIST returns the #VALUE! error.
- If x < 0, GAMMADIST returns the #NUM! error.
- If alpha ≤ 0 or beta ≤ 0, GAMMADIST returns the #NUM! error.
- In Excel 2007, this is a Statistical function