Purpose
Return value
Syntax
=GAMMAINV(probability,alpha,beta)
- probability - The probability associated with the gamma distribution (must be between 0 and 1).
- alpha - The shape parameter of the distribution.
- beta - The scale parameter of the distribution.
Using the GAMMAINV function
The GAMMAINV function returns the value at which the cumulative gamma distribution reaches a specified probability. For better accuracy and consistency with other modern statistical functions, it is recommended to use the GAMMA.INV function . GAMMA.INV uses the same arguments and provides the same core functionality with improved numerical precision. See the GAMMA.INV function for more details and examples.
Notes
- GAMMAINV is a legacy function. For Excel 2010 and later, use the GAMMA.INV function.
- If any argument is non-numeric, GAMMAINV returns the #VALUE! error.
- If probability < 0 or ≥ 1, GAMMAINV returns the #NUM! error.
- If alpha ≤ 0 or beta ≤ 0, GAMMAINV returns the #NUM! error.
- GAMMA.INV provides improved accuracy over the legacy GAMMAINV function.
Purpose
Return value
Syntax
=GAMMALN(x)
- x - A positive real number for which you want to calculate the natural logarithm of the gamma function.
Using the GAMMALN function
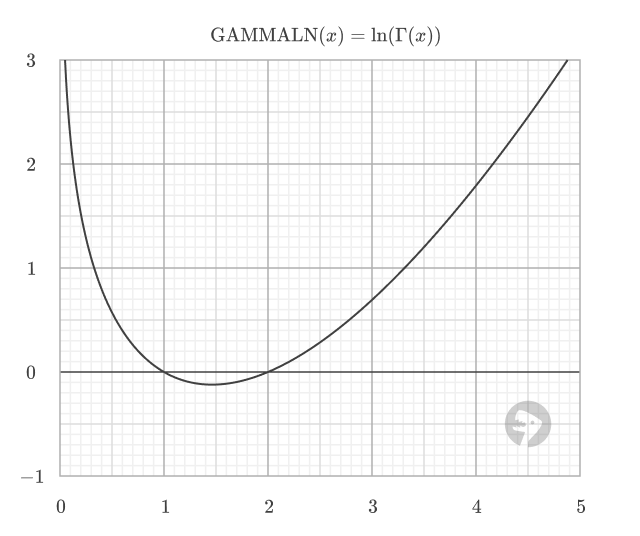
The GAMMALN function returns the natural logarithm of the gamma function, ln(Γ(n)), for a given number. This is especially useful in statistical calculations, such as those involving probability distributions, where the gamma function appears in the denominator and direct computation could result in very large or very small numbers. For positive integers n, GAMMALN(n) is equivalent to LN((n-1)!).
For example, the following formula calculates the natural logarithm of the gamma value for 5:
=GAMMALN(5) // returns 3.17805383
Key features
Returns the natural logarithm of the gamma function for decimal numbers
For positive integers n, GAMMALN(n) equals LN((n-1)!)
Accepts positive decimal numbers as input
Returns #NUM! error for zero and negative numbers
Key features
Example #1 - Basic calculations
Example #2 - Relationship to gamma and factorials
Example #3 - Error conditions
Formula definition
GAMMALN is still available for compatibility with earlier versions of Excel, but has been replaced by GAMMALN.PRECISE , which provides improved accuracy. Microsoft recommends using GAMMALN.PRECISE for new work.
Example #1 - Basic calculations
The GAMMALN function takes a single argument as input like this:
=GAMMALN(x)
The argument x is the value for which you want to calculate the natural logarithm of the gamma function. Here are some basic examples showing both integer and non-integer inputs:
=GAMMALN(0.5) // returns 0.57236494...
=GAMMALN(2.0) // returns 0
=GAMMALN(2.5) // returns 0.28468287...
=GAMMALN(4.0) // returns 1.79175947...
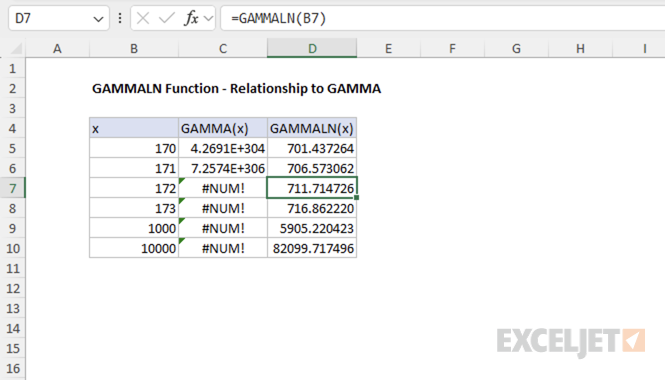
Example #2 - Relationship to gamma and factorials
In general, the GAMMALN function is equivalent to the natural logarithm of the GAMMA function :
=GAMMALN(x) // returns LN(GAMMA(x))
This relationship makes the GAMMALN function useful for calculations involving large factorials, as it avoids direct computation of large numbers. For example, attempting to compute a large factorial directly with the GAMMA function can result in an error due to overflow:
=GAMMA(172) // returns #NUM! error
In contrast, using GAMMALN allows you to work with the logarithm of the gamma function, which avoids this problem and provides a valid result even for large inputs.
Example #3 - Error conditions
The GAMMALN function returns #NUM! for zero and negative numbers, and #VALUE! for non-numeric inputs.
=GAMMALN(0) // returns #NUM! error
=GAMMALN(-1) // returns #NUM! error
=GAMMALN(-2.5) // returns #NUM! error
=GAMMALN("text") // returns #VALUE! error
Formula definition
The GAMMALN function is defined as the natural logarithm of the gamma function. Shown below is the plot of the GAMMALN function, where Γ(x) is the gamma function.