Purpose
Return value
Syntax
=GAMMALN.PRECISE(x)
- x - A positive real number for which you want to calculate the natural logarithm of the gamma function.
Using the GAMMALN.PRECISE function
The GAMMALN.PRECISE function returns the natural logarithm of the gamma function, ln(Γ(n)), for a given number. This is useful in statistical calculations, such as those involving probability distributions, where the gamma function appears in the denominator and direct computation could result in very large or very small numbers.
For positive integers n, GAMMALN.PRECISE(n) is equivalent to LN((n-1)!). For example, the following formula calculates the natural logarithm of the gamma value for 5:
=GAMMALN.PRECISE(5) // returns 3.17805383
Key features
Returns the natural logarithm of the gamma function for decimal numbers
For positive integers n, GAMMALN.PRECISE(n) equals LN((n-1)!)
Accepts positive decimal numbers as input
Returns #NUM! error for zero and negative numbers
More accurate than the legacy GAMMALN function
Key features
Example #1 - Basic calculations
Example #2 - Relationship to gamma and factorials
Example #3 - Error conditions
Formula definition
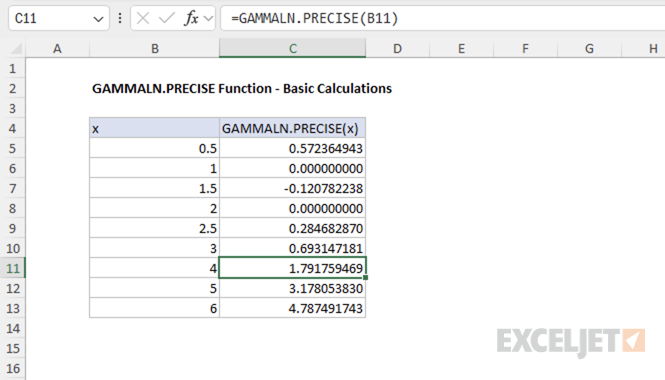
Example #1 - Basic calculations
The GAMMALN.PRECISE function takes a single argument as input like this:
=GAMMALN.PRECISE(x)
The argument x is the value for which you want to calculate the natural logarithm of the gamma function. Here are some basic examples showing both integer and non-integer inputs:
=GAMMALN.PRECISE(0.5) // returns 0.57236494...
=GAMMALN.PRECISE(2.0) // returns 0
=GAMMALN.PRECISE(2.5) // returns 0.28468287...
=GAMMALN.PRECISE(4.0) // returns 1.79175947...
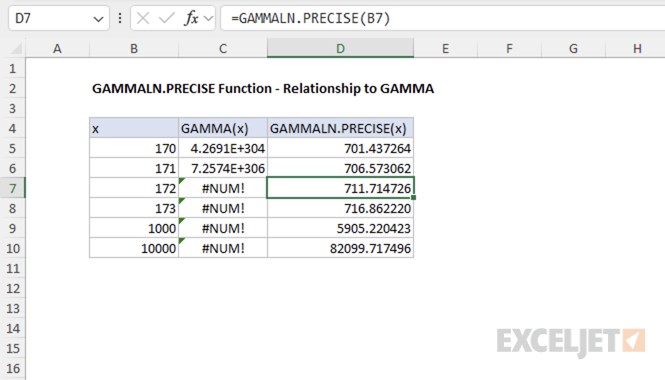
Example #2 - Relationship to gamma and factorials
In general, the GAMMALN.PRECISE function is equivalent to the natural logarithm of the gamma function:
=GAMMALN.PRECISE(x) // returns LN(GAMMA(x))
This relationship makes the GAMMALN.PRECISE function useful for calculations involving large factorials, as it avoids direct computation of large numbers. For example, attempting to compute a large factorial directly with the GAMMA function can result in an error due to overflow:
=GAMMA(172) // returns #NUM! error
In contrast, using GAMMALN.PRECISE allows you to work with the logarithm of the gamma function, which avoids this problem and provides a valid result even for large inputs.
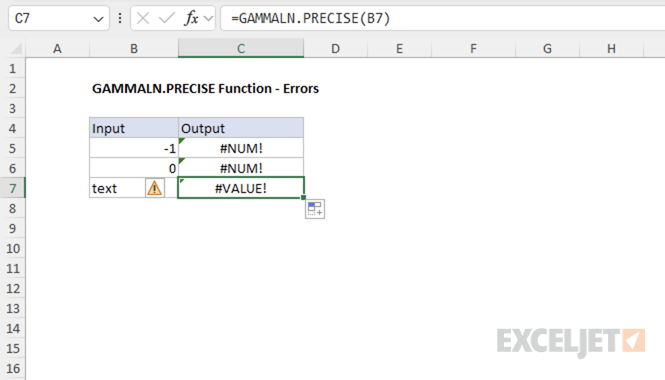
Example #3 - Error conditions
The GAMMALN.PRECISE function returns #NUM! for zero and negative numbers, and #VALUE! for non-numeric inputs.
=GAMMALN.PRECISE(0) // returns #NUM! error
=GAMMALN.PRECISE(-1) // returns #NUM! error
=GAMMALN.PRECISE(-2.5) // returns #NUM! error
=GAMMALN.PRECISE("text") // returns #VALUE! error
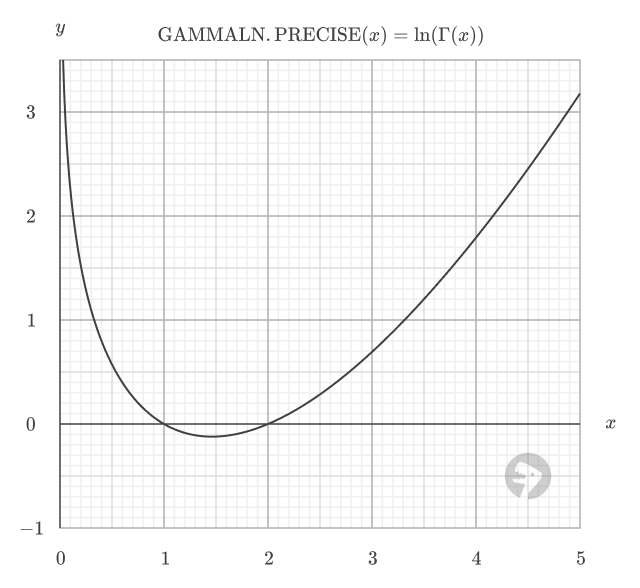
Formula definition
The GAMMALN.PRECISE function is defined as the natural logarithm of the gamma function. The function is mathematically equivalent to:
GAMMALN.PRECISE(x) = LN(GAMMA(x))
The function is plotted below, where Γ(x) is the gamma function.
Purpose
Return value
Syntax
=GEOMEAN(number1,[number2],...)
- number1 - First value or reference.
- number2 - [optional] Second value or reference.
Using the GEOMEAN function
The Excel GEOMEAN function calculates the geometric mean . Geometric mean is the average of a set of products — technically, the nth root of n numbers. The general formula for the geometric mean of n numbers is the nth root of their product. The equation looks like this:
For example, given two numbers, 4 and 9, the long-hand calculation for the geometric mean is 6:
=(4*9)^(1/2)
=(36)^(1/2)
=6
The GEOMEAN function returns the same result:
=GEOMEAN(4,9) // returns 6
By contrast, the arithmetic mean is 6.5:
=(4+9)/2=6.5
The GEOMEAN function takes multiple arguments in the form number1 , number2 , number3 , etc. up to 255 total. Arguments can be a hardcoded constant, a cell reference, or a range. Often, a single range or array is used instead of multiple arguments, as seen in the example worksheet.
Examples
In the example shown, GEOMEAN is used to calculate a compound annual growth rate. To do this we use the growth factor values in column D in the GEOMEAN function, then subtract 1. The formula in G7 is:
=GEOMEAN(D6:D10)-1
Notes
- Arguments can be numbers, names, arrays, or references that contain numbers.
- Empty cells, and cells that contain text or logical values are ignored.
- If any provided values are less than or equal to zero, GEOMEAN returns #NUM!