Purpose
Return value
Syntax
=IMDIV(complex_num1,complex_num2)
- complex_num1 - The first complex number.
- complex_num2 - The second complex number.
Using the IMDIV function
The Excel IMDIV function returns the quotient of two complex numbers. For example, given “-7+11i” and “3+5i” as input, the function returns the quotient “1+2i”, which is the result of dividing the first number by the second.
=IMDIV(COMPLEX(-7,11),COMPLEX(3,5)) // returns 1+2i
The quotient of two complex numbers can be visualized by uniformly stretching and rotating the coordinate system so that “1” goes to the complex number, which is the divisor. In this case, the transformed coordinate system (shown in blue) is stretched and rotated so that “1” (shown as the green arrow) goes to the point “3+5i”. The quotient represents how to get to the first complex number, “-7 +11i”, in terms of the transformed coordinates.
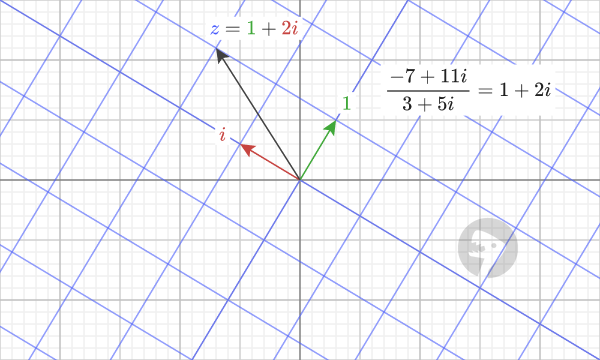
Here’s another example: the result of dividing “-14-2i” by “4+2i” is equal to “-3+i”.
=IMDIV(COMPLEX(-14,-2),COMPLEX(4,2)) // returns -3+i
If we uniformly stretch and rotate the coordinate system so that the green arrow, “1”, goes to the point “4+2i”, we can see that to get to the point “-14-2i” we travel “-3+i” units in the transformed coordinate system.
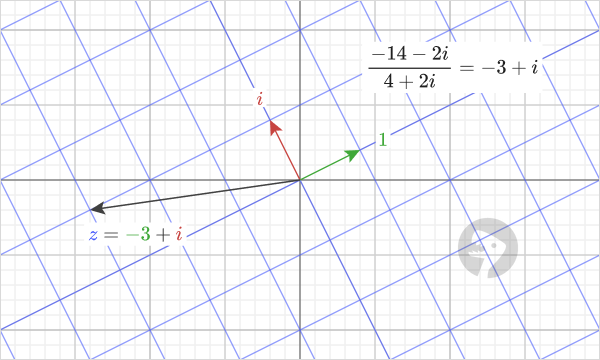
We can visualize the example that corresponds to this one by switching the divisor with the quotient. In other words, the result of dividing “-14-2i” by “-3+i” is equal to “4+2i”.
=IMDIV(COMPLEX(-14,-2),COMPLEX(-3,1)) // returns 4+2i
When we uniformly stretch and rotate the coordinate system so that the green arrow, “1”, goes to the point “-3+i”, now we travel “4+2i” units in the transformed coordinate system to get to the point “-14-2i”.
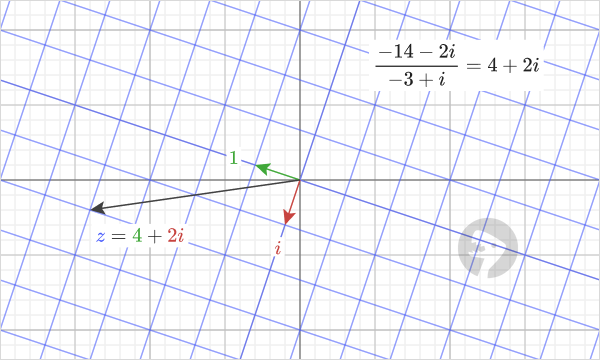
Explanation
When dividing complex numbers, it’s not obvious how to calculate the result by hand.

Compare this to complex multiplication, where we can use algebra to multiply two complex numbers.

The key to dividing two complex numbers is to convert the problem into one we know how to solve. This is done by using the fact that multiplying a complex number by its conjugate equals a real number.

This changes the denominator into a real number, which we know how to divide by. This is how we can manually calculate the quotient of two complex numbers in Excel.
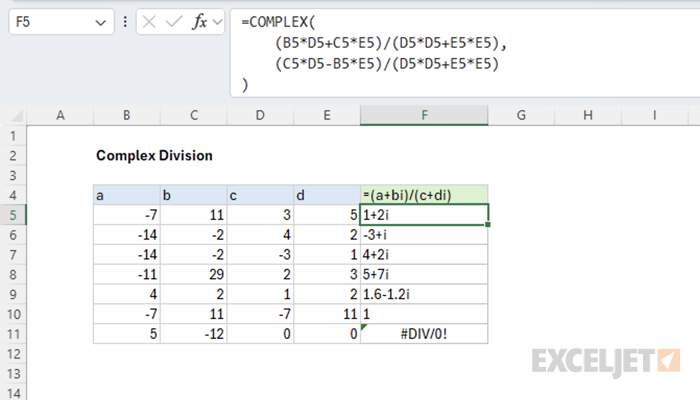
There is a slight difference between this formula and the IMDIV function because IMDIV returns a #NUM! error instead of #DIV/0! when dividing by zero.
Images courtesy of wumbo.net .
Purpose
Return value
Syntax
=IMEXP(complex_num)
- complex_num - The complex number in the form “x+yi”.
Using the IMEXP function
The Excel IMEXP function returns the exponential of a complex number. For example, given “0+πi” as input, the function returns “-1+3.23108914886517E-15i” as output. The output is essentially -1, but due to floating point precision, it contains a very small imaginary component.
=IMEXP(COMPLEX(0,PI())) // returns -1 + 3.23108914886517E-15i
Given real number input, the function behaves like the exponential function and models exponential growth.
=IMEXP(COMPLEX(1,0)) // returns 2.71828182845905
Given imaginary input representing an angle, the function returns the corresponding point on the unit circle in the complex plane.
=IMEXP(COMPLEX(0,PI()/3)) // returns cos(π/3) + sin(π/3)i
Notation
The complex exponential function often appears as the Latin letter e to some power. This notation is equivalent to passing the complex number as input to the exponential function.

In Excel, we write the exponential of a complex number “z=x+yi” like this:
=IMEXP(COMPLEX(x,y))
Euler’s Formula
The complex exponential function appears in a famous math formula called “Euler’s Formula,” which relates i, π, and -1 together.

We can write another version of this formula that better describes what’s happening in terms of the angle θ.

Given imaginary input representing an angle, the function returns the corresponding point on the unit circle in the complex plane. For example, given the input “i π/3” the function returns the point on the unit circle corresponding to the angle of π/3 radians.

In Excel, we can see this behavior in the following formula:
=IMEXP(COMPLEX(0,PI()/3)) // returns 0.5 + 0.866025404i
Explanation
In math, the exponential of a complex number can be expanded using the additive property of exponentials.

The right expression can be expanded further using Euler’s Formula.

In Excel, the complex exponential function is equivalent to this formula.
=IMPRODUCT(
COMPLEX(EXP(x), 0),
COMPLEX(COS(y), SIN(y))
)
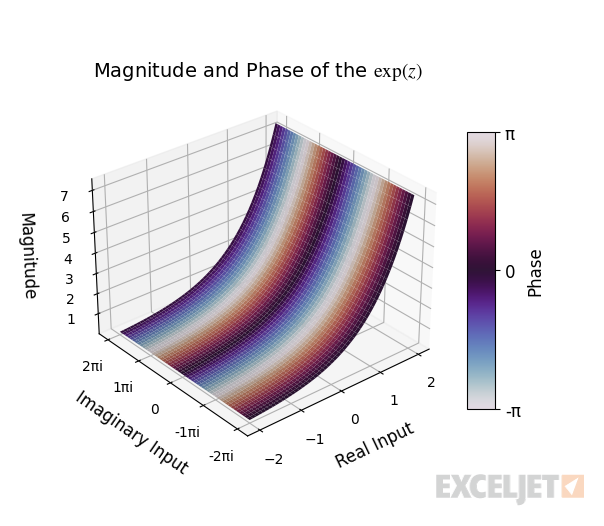
From this, we can see the real part of the input governs the magnitude of the output, and the imaginary part of the input governs the phase (angle) of the output. For example, given the input “2+π/3”, the function returns a complex number with a magnitude of EXP(2) and an angle of π/3 radians.
=IMEXP(COMPLEX(2,PI()/3)) // returns 3.694528049 + 6.399110292i
We can draw the returned complex number in the complex plane like this.

In general, the function’s output can be visualized with the 3D plot below. The horizontal XY plane represents input in the complex plane, and the vertical axis represents the magnitude of the output. The plot’s surface is colored using the output’s phase (angle).
Polar Form
The complex exponential function can express a complex number in its polar form by describing the number in terms of its radius and angle.
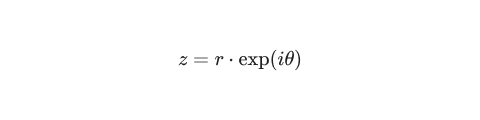
For example, to write the complex number z in Excel with a radius of 5 and an angle of π/4, we scale the point on the complex unit circle given by EXP(iθ) by the radius like this:
=IMPRODUCT(
COMPLEX(5,0),
IMEXP(COMPLEX(0,PI()/4))
) // returns 3.535533906 + 3.535533906i
We can draw this complex number on the complex plane to visualize its coordinates.

Inverse
The inverse of the complex exponential function is the complex natural logarithm. For example, if we pass the output of the exponential function for “2+πi” to the natural logarithm, we get “2+πi” as a result.
=IMLN(IMEXP(COMPLEX(2,PI()))) // returns 2 + πi
In general, given a complex number, the natural logarithm function returns the natural logarithm of the radius of the number for the real part and the angle of the number for the imaginary part.

Sometimes, this can result in a branch cut, where a different-but-equivalent angle is returned instead.
=IMLN(IMEXP(COMPLEX(2,3*PI()))) // returns 2 + πi
This is discussed in more depth in the complex natural logarithm article.
Images courtesy of wumbo.net .