Purpose
Return value
Syntax
=LCM(number1,[number2],...)
- number1 - The first number.
- number2 - [optional] The second number.
Using the LCM function
The LCM function returns the least common multiple of two or more numbers. The least common multiple is the smallest positive integer that is a multiple of all numbers supplied. Least common multiple is also known as the “least common denominator”, and the “lowest common denominator”.
The LCM function takes one or more arguments called number1 , number2 , number3 , etc. All numeric values are expected to be integers. Numbers with decimal values will be truncated to integers before a result is calculated. Each argument can be a hardcoded constant, a cell reference, or a range that contains multiple values. The LCM function can accept up to 255 arguments total.
Examples
The least common multiple of 3 and 4 is 12, since 12 is the smallest multiple of both 3 and 4:
=LCM(3,4) // returns 12
The least common multiple of 3, 4, and 5 is 60, since 60 is the smallest multiple of all three numbers:
=LCM(3,4,5) // returns 60
Worksheet example
In the example worksheet shown above, we are using two slightly different formulas to calculate the lowest common multiple. The first formula provides two separate cell references, and the second formula uses a single range that contains three values. In rows, 5 to 10, there are two values in columns B and C, and the formula in F5:F10 (copied down) is:
=LCM(B5,C5) // 2 cell references
In rows 11 to 15, there are three values in columns B, C, and D. The formula in F11:F15 (copied down) is:
=LCM(B11:D11) // range with 3 values
Because the LCM function evaluates empty cells as zero, the result returned by LCM will be zero if any cell references are empty. Therefore, it’s important not to include empty cell references.
Notes
- LCM evaluates empty cells as zero.
- LCM works with integers; decimal values are removed before calculation.
- If arguments contain a non-numeric value. LCM returns the #VALUE! error.
- To calculate the greatest common divisor, see the GCD function .
Purpose
Return value
Syntax
=LN(number)
- number - A number to take the natural logarithm of.
Using the LN function
The LN function returns the natural logarithm of a given number. The natural logarithm is equivalent to log base e of a number, where e is Euler’s number , a mathematical constant with the approximate value 2.71828182845904. The LN function is the inverse of the EXP function and is used to model exponential decay.
The LN function takes just one argument, number , which should be a positive number.
Examples
=LN(1) // returns 0
=LN(e) // returns 1
=LN(e^2) // returns 2
The equivalent form of the natural logarithm function is given by:
=LN(number)=LOG(number,e) // Where e ≈ 2.7128 or EXP(1)
Graphs
Below is a graph of the natural log logarithm:
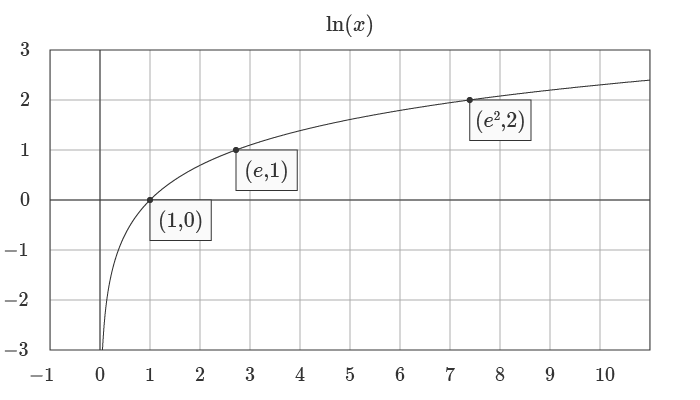
The natural logarithm function and exponential function are the inverse of each other, as you can see in the graph below:
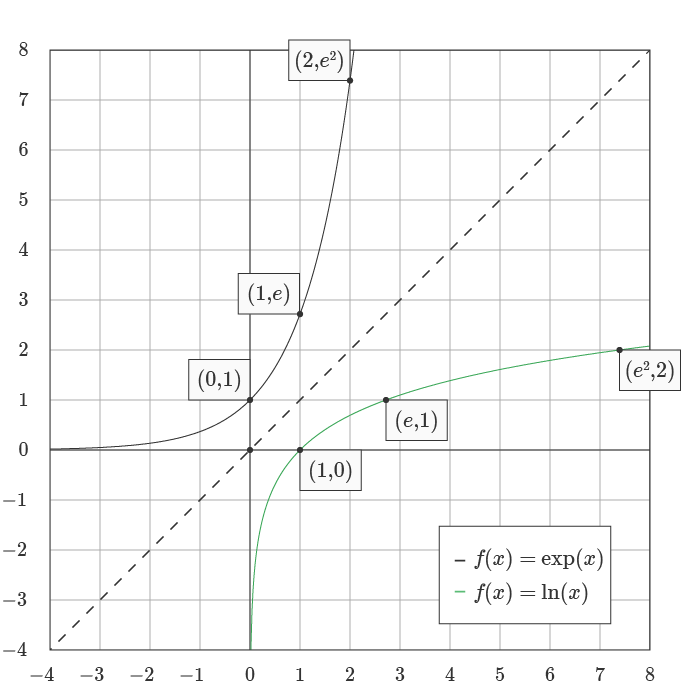
This inverse relationship can be represented with the formulas below, where the input to the LN function is the output of the EXP function :
= LN(EXP(1)) // returns 1
= LN(EXP(2)) // returns 2
= LN(EXP(n)) // returns n
See wumbo.net for a more detailed explanation of key math concepts and formulas.
Notes
- The natural logarithm function can be defined as the area under a hyperbola.
- The function is used in applications relating to compound interest.