If you’ve generated random numbers in Excel before, you’ll know there’s a limitation where, every time you make a change to the spreadsheet, functions like RAND , RANDBETWEEN , and RANDARRAY recalculate and return different values. In Excel lingo, functions with this behavior are called volatile functions .
This volatility can be frustrating when you need random results to stay put. Fortunately, there’s a solution: a seeded random number generator. In this article, we’ll show you how to build one using Excel’s LAMBDA function, giving you full control over when your random numbers change. We’ll start by looking at the problem in detail, then walk through building a custom function step by step.
- The problem with random formulas
- What is a seeded random number generator?
- Benefits of seeded random numbers
- Our approach
- The RNG algorithm
- Implementing the LAMBDA function
- Improving the formula
- Creating a custom HASH function
- Sorting students with RAND_SEQUENCE
- Using RAND_SEQUENCE in your workbooks
The problem with random formulas
To illustrate the problem with random formulas in Excel clearly, let’s look at an example. Imagine a teacher wants to randomly assign students to groups every month. One simple way to do this is to set up the groups in one column and, in the next column, sort the students randomly. You can see this approach in the workbook below, where the original list of students is in column B, the list of groups is in column D, and the randomly sorted students are in column E. The formula in cell E5 looks like this:
=SORTBY(B5:B13,RANDARRAY(ROWS(B5:B13)))

See Random list of names for details about how this formula works.
At first glance, everything looks great. We have successfully placed 9 students into 3 groups using a random sort. However, the problem is that RANDARRAY is a volatile function, which means it will recalculate each time the worksheet changes. You can see how this works in the screens below, where three unrelated edits cause the formula to return new results:
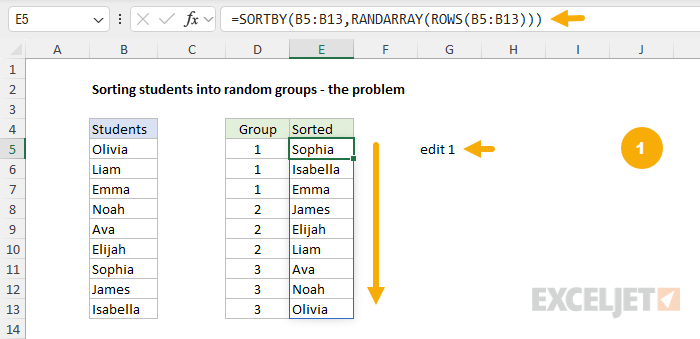

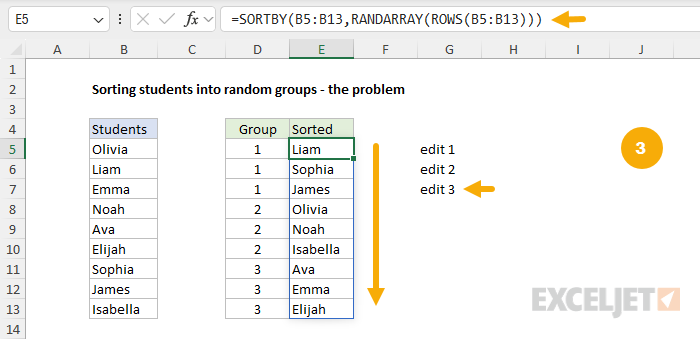
Every change to the worksheet creates new random groups!
The classic solution to this problem is to copy the randomly sorted students to the clipboard and use Paste Special > Values to create static values that won’t change. However, this is an annoying workaround, since it requires several manual steps, and it also destroys the formulas used to generate random results in the first place. What we really want is a way to generate new random numbers on demand .
This is not a new problem. For most programming languages, there exists a tried and true solution used when generating random numbers called seed values . It works like this: when you initialize a random number generator with a seed value, you get reproducible random numbers based on the seed value . The key idea here is reproducible , meaning two separate calls with the same seed value will produce the same random numbers . The solution is a Seeded Random Number Generator, sometimes abbreviated to “RNG”.
What is a seeded random number generator?
A seeded random number generator creates numbers that look random but come from a repeatable process. You give it a starting value called a seed, and it uses that seed to produce a sequence of random-looking numbers. Use the same seed again, and you get the exact same sequence. Change the seed, and you get a completely different sequence. Random number generators are built with specific algorithms and are used in almost every programming environment and platform. Excel’s built-in random functions don’t let you choose a seed, so results change whenever the worksheet recalculates. A seeded generator fixes that by giving you stable, reproducible random numbers that won’t change with every worksheet change.
Benefits of seeded random numbers
As shown above, Excel’s built-in random functions are volatile and recalculate with each workbook change. Having a seeded random number generator available in Excel offers important benefits, including:
- On-demand generation of new random values based on a seed.
- Stable random results that don’t recalculate when workbooks are opened or edited.
- Repeatable results with the same seed value.
- Better performance by avoiding excessive recalculation.
- Reproducible worksheet demos.
These benefits allow you to build stable and reproducible worksheets that do things like:
- Randomly assign students to groups at the start of every month.
- Randomly pick winners in a prize drawing.
- Simulate random events in financial modeling or risk analysis.
- Create reproducible dice rolls or card shuffles.
- Generate random lists of names, products, countries, sizes, etc
In short, a seeded Random Number Generator is valuable in Excel because it gives you “reproducible randomness”—something Excel’s built-in random functions cannot provide.
Our Approach
We are going to implement a random number generator in Excel by writing a LAMBDA function and naming it RAND_SEQUENCE in the name manager. Our function will take two arguments:
- seed - a text string representing the seed value.
- n - a number indicating how many random values to return.
When we’re finished, we’ll be able to call our new function like any other Excel function, and it will return random decimal values. For example, if we call RAND_SEQUENCE with the seed “apple” and the number 3, we’ll get back numbers like this:
=RAND_SEQUENCE("apple",3) // returns {0.710028;0.444729;0.560484}
And, when we call the function again somewhere else in the spreadsheet and pass in the same seed value, we’ll get the same random values:
=RAND_SEQUENCE("apple",3) // returns {0.710028;0.444729;0.560484}
In other words, the function returns random numbers, but these numbers are uniquely determined by the seed value passed into the function. To generate a new sequence of random numbers, we pass in a different seed value. This is what makes a function like this so useful and is exactly what the teacher in our scenario could use to reassign students into groups at the start of every month.
This approach is made possible by the new LAMBDA functions introduced in Excel over the past few years, including LET , LAMBDA , MAP , SCAN , REDUCE , and more . These functions really expand what’s possible in Excel by unlocking new ways to tackle hard problems. In our case, implementing a seeded random number generator is an excellent example of how these functions can be used to create a useful new feature that can be used just like a built-in Excel function.
The RNG algorithm
There are many different ways to implement a seeded random number generator. We are going to write a formula that uses the Park-Miller “minimal standard” LCG algorithm , because it’s well-documented and straightforward to implement.
The way this algorithm works is by performing a series of multiplications and mod operations on an initial seed value. For example, starting with an integer seed value, we multiply it by a=16807 and then take the remainder of dividing the result by m=2147483647 using the MOD function. This gives us a random integer between zero and the value of m . To generate the next random integer, we use the previous result as the seed value and repeat the process.
For example, to generate the first integer using a seed value of 42 we calculate the result of MOD(a*42, m) like this:
=LET(
seed,42,
a,16807,
m,2147483647,
MOD(a*seed,m)
) // returns 705894
Then, to generate the next integer, we pass in 705894 as the current seed value and perform the same operation: multiply by a and take the remainder of dividing by m .
=LET(
seed,705894,
a,16807,
m,2147483647,
MOD(a*seed,m)
) // returns 1126542223
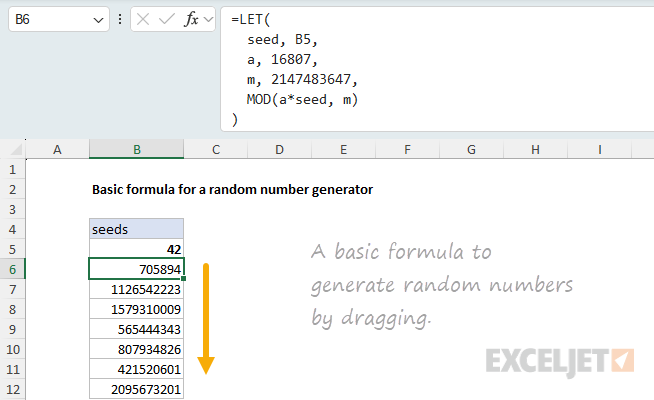
And so on. The screenshot below shows how this formula can be adapted to generate values in Excel. Notice that the seed value is defined as the value in the cell above, starting at B5. As the formula in B6 is dragged down, it generates the sequence of random integers seen below:
To normalize this sequence of random integers to numbers between zero and one, we can divide by the value of m=2147483647 like this:
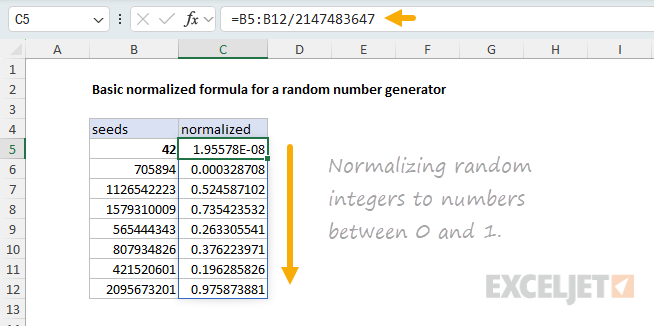
This gives us a seeded sequence of random numbers using the Park-Miller algorithm. Now you could use this formula as-is in a helper column, but what we want to do is convert this to a LAMBDA function that takes in a seed and quantity as arguments and spills the random numbers. There are a number of benefits to doing this:
- Naming the function in the name manager makes it so we can use it elsewhere in the spreadsheet and abstracts the implementation details from the user.
- Having a function that spills the results removes the need for a helper column and makes the random number generator more practical to use.
- The arguments can be normalized to prevent errors.
The end result will be a function that takes in a seed value and quantity as arguments and spills the random numbers. This is similar to the behavior of RANDARRAY , except our function allows us to control when the random numbers are generated.
Implementing the LAMBDA function
First, let’s create a formula that has the spill behavior that we want. Once we get that working, we’ll wrap it in a LAMBDA and give it a name in the name manager.
To start, we’ll use the SCAN function to generate a sequence of seed values. The syntax of the SCAN function looks like this:
=SCAN([initial_value],array,lambda)
- initial_value (optional): The starting value for the accumulation.
- array: The array (range or constant array) to process.
- lambda(accumulator, value): A custom function that defines how to combine the running total (accumulator) with each element (value).
The way SCAN works is it processes each element of the array. At each step:
- The accumulator holds the running result so far
- The value is the current element from the array
- The LAMBDA function is called with the current value of the accumulator and the current element from the array to calculate the next value of the accumulator
For example, the following formula generates a running total for the input array {1; 2; 3} generated by the SEQUENCE function:
=SCAN(0,SEQUENCE(3),LAMBDA(acc,val,acc+val)) // returns {1;3;6}
The key feature of SCAN is that it outputs an array of running results for each step , which is the spill behavior we want. In other words, the length of the input array controls how many times the lambda function is called, so our basic setup looks something like this:
=LET(
seed,42,
n,5,
step,LAMBDA(...)
SCAN(seed,SEQUENCE(n),step)
)
We call SCAN with the initial seed value and an array whose length is equal to the number of random integers to generate. The step function will implement the logic from earlier to calculate the next seed value using the current seed value.
For example, to generate the first three values, set up the formula like this with the seed=42 and n=3 :
=LET(
seed,42,
n,3,
a,16807,
m,2147483647,
step,LAMBDA(s,_,MOD(a*s,m)),
SCAN(seed,SEQUENCE(n),step)
) // returns {705894;1126542223;1579310009}
This formula returns the same sequence of integers as before: {705894; 1126542223; 1579310009} .
To understand how SCAN works in this context, let’s trace through the chain of calls to the lambda function. When we call SCAN(seed, SEQUENCE(3), step) , the lambda function step gets called three times with the following arguments:
- step(42, 1) → returns 705894
- step(705894, 2) → returns 1126542223
- step(1126542223, 3) → returns 1579310009
The lambda function calculates the next seed value by multiplying the current seed value by a=16807 and taking the remainder of dividing by m=2147483647 using the MOD function. For each call, the result is passed to the next call to be used as the seed value represented by the argument s . This is why the first argument of the lambda function is called an accumulator, because it gets passed between each call.
Note: We don’t actually use the values in the array generated by SEQUENCE. This is why the second argument of the step lambda function is named with an underscore symbol (_) to indicate that the value is never used. What’s important about the input array is that it controls how many times the step lambda function is called.
As before, to normalize these random numbers to be in the range from zero to one, we divide by the value of m .
=LET(
seed,42,
n,5,
a,16807,
m,2147483647,
step,LAMBDA(s,_,MOD(a*s,m)),
results,SCAN(seed,SEQUENCE(n),step),
results/m
)
This formula generates a sequence of random numbers based on the seed value, where n=5 controls how many values are generated.

To convert this into a lambda function, wrap the formula in a lambda function and change seed and n to be parameters of the lambda function. For example, the following formula is equivalent to the previous version that uses LET:
=LAMBDA(seed,n,
LET(
a,16807,
m,2147483647,
step,LAMBDA(s,_,MOD(a*s,m)),
results,SCAN(seed,SEQUENCE(n),step),
results/m
)
)(42,5)
Here we are invoking our lambda function and passing in seed=42 and n=5 as input, which is a good way to test and tweak the lambda function before adding it to the name manager. When we add the formula to the name manager, we’ll remove the (42, 5) which is a special syntax used to call the function before it has a name. To name the formula, go to Formulas > Name Manager > New and enter RAND_SEQUENCE for the name and then enter the following formula for the value:
=LAMBDA(seed,n,
LET(
a,16807,
m,2147483647,
step,LAMBDA(s,_,MOD(a*s,m)),
results,SCAN(seed,SEQUENCE(n),step),
results/m
)
)
After adding the formula to the name manager, you should see the function in the name manager like this:
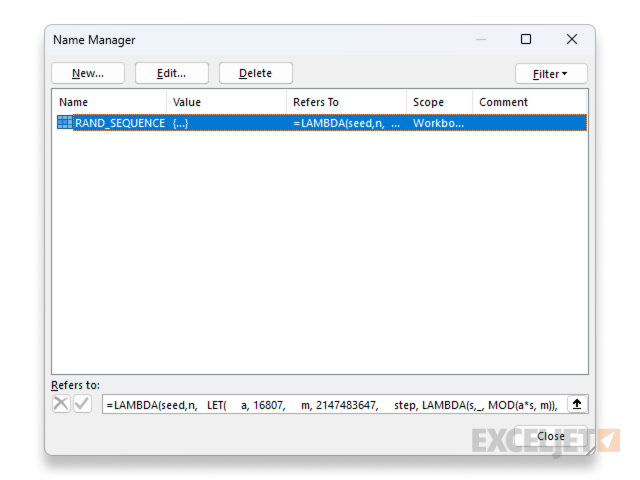
Now we can use the RAND_SEQUENCE function in the spreadsheet like this to generate a sequence of 10 random numbers using a seed value.

Improving the formula
This is a good start, but there are some improvements we should make to make the function more robust and user-friendly. To begin with, we should normalize the seed value so it is an integer greater than zero and less than m . This prevents some issues that can arise if the seed value is zero or greater than m . To do this, modify the formula by introducing a new variable start that gets set to the normalized seed value:
=LAMBDA(seed,n,
LET(
a,16807,
m,2147483647,
start,IF(INT(seed)=0,1,MOD(INT(seed),m)),
step,LAMBDA(s,_,MOD(a*s,m)),
results,SCAN(start,SEQUENCE(n),step),
results/m
)
)
The second improvement addresses some more subtle issues.
- If the seed value is small, say in the range of 1-100 , the first random number will always be a relatively small number.
- Because of how the algorithm works, adjacent seed values produce similar sequences of random numbers. This isn’t a huge issue, but it is noticeable if using adjacent seed values like 42 and 43 to sort a list.
These issues can be avoided by using seed values that are evenly distributed across the range of 1 to m , but this is a bit of a hassle for the user. We can address both of these issues with a hash function.
Creating a custom HASH function
A simple way to handle the issues mentioned above is to introduce a “hash” function in the name manager and use it to generate seed values. Hash functions are another example of a well-understood and useful concept that can be implemented in Excel using the new lambda functions. Simply put, a hash function takes in a string and returns a number.
What this means for our RAND_SEQUENCE function is that we can pass a string instead of an integer to be used as the seed value. This will resolve both issues. The hash function will produce a suitably large integer for the seed value, and make it easy for the user to avoid adjacent seed values.
The following formula implements a hash function (DJB2) that takes in a string and returns a number. For example, given the string “apple” , the hash function returns the number 253337143 :
=LAMBDA(str,
LET(
s,TEXT(str,"@"),
bytes,UNICODE(MID(s,SEQUENCE(LEN(s)),1)),
h0,5381,
step,LAMBDA(h,c,MOD(h*33+c,2^32)),
REDUCE(h0,bytes,step)
)
)("apple") // returns 253337143
As before, to create a new custom function, we open the Name Manager at Formulas > Name Manager > New and enter HASH for the name and the lambda function above for the value. Now we can use the new HASH function like this:
=HASH("apple") // returns 253337143
=HASH("orange") // returns 319921761
To incorporate the HASH function into the RAND_SEQUENCE function, we use it to normalize the seed value like this:
=LAMBDA(seed,n,
LET(
a,16807,
m,2147483647,
h,HASH(seed),
start,IF(INT(h)=0,1,MOD(INT(h),m)),
step,LAMBDA(s,_,MOD(a*s,m)),
results,SCAN(start,SEQUENCE(n),step),
results/m
)
)
Now we have a robust and user-friendly random number generator that can be used to generate reproducible random numbers using a seed value like “apple” or “orange”.
=RAND_SEQUENCE("apple",10) // spills ten random numbers

Sorting students with RAND_SEQUENCE
To use the custom RAND_SEQUENCE function to sort students into groups, we can adapt our original random sort formula above to use random numbers generated by the RAND_SEQUENCE function instead of RANDARRAY:
=SORTBY(range,RANDARRAY(ROWS(range)))
Becomes:
=SORTBY(range,RAND_SEQUENCE(ROWS(range)))
A final touch is to wrap the formula in the LET function so that we only refer to the range once. You can see how this works in the worksheet below, where the following formula sorts the students in B3:B11 with the seed value of “apple” in G3 .
=LET(
students,B3:B11,
SORTBY(students,RAND_SEQUENCE(G3,ROWS(students)))
)
<img loading=“lazy” src=“https://exceljet.net/sites/default/files/styles/original_with_watermark/public/images/articles/inline/random_number_generator_sort_students_apple.png" onerror=“this.onerror=null;this.src=‘https://blogger.googleusercontent.com/img/a/AVvXsEhe7F7TRXHtjiKvHb5vS7DmnxvpHiDyoYyYvm1nHB3Qp2_w3BnM6A2eq4v7FYxCC9bfZt3a9vIMtAYEKUiaDQbHMg-ViyGmRIj39MLp0bGFfgfYw1Dc9q_H-T0wiTm3l0Uq42dETrN9eC8aGJ9_IORZsxST1AcLR7np1koOfcc7tnHa4S8Mwz_xD9d0=s16000';" alt=“Random groups with the seed value “apple” - 11”>
Now that we have a seeded random number determining the sort order, the results will not change when routine edits are made to the worksheet. Only the seed value in G3 controls the output — other changes in the workbook will not cause the formula to generate new results. When we change the seed value in G5 to “orange”, the formula will sort the students in a different random order:
<img loading=“lazy” src=“https://exceljet.net/sites/default/files/styles/original_with_watermark/public/images/articles/inline/random_number_generator_sort_students_orange.png" onerror=“this.onerror=null;this.src=‘https://blogger.googleusercontent.com/img/a/AVvXsEhe7F7TRXHtjiKvHb5vS7DmnxvpHiDyoYyYvm1nHB3Qp2_w3BnM6A2eq4v7FYxCC9bfZt3a9vIMtAYEKUiaDQbHMg-ViyGmRIj39MLp0bGFfgfYw1Dc9q_H-T0wiTm3l0Uq42dETrN9eC8aGJ9_IORZsxST1AcLR7np1koOfcc7tnHa4S8Mwz_xD9d0=s16000';" alt=“Random groups with the seed value “orange” - 12”>
Even better, the random sort is reproducible: if you change the seed value back to “apple”, you again see the random sort associated with that seed. In other words, you can easily reproduce the first random sort.
This is exactly what we set out to do. We have a function that takes in a seed value and quantity as arguments and spills random numbers. This is a significant upgrade to the volatile results that Excel’s random functions generate, and very handy in any situation where you need stable and reproducible random results.
Using RAND_SEQUENCE in your workbooks
You might wonder how you can easily define the two custom functions explained above, RAND_SEQUENCE and HASH in your own workbooks without recreating them from scratch with the Name Manager. This is not difficult. The Excel workbook attached to this article contains the RAND_SEQUENCE function and the HASH function already defined and ready to use. To quickly copy these functions into your own workbook, follow these steps:
- Go to Sheet8 in the workbook, which uses the final function
- Right-click the sheet name and select “Move or Copy…”
- For “To book”, select an existing (or new) workbook.
- Tick the “Create a copy” checkbox to leave the original sheet intact.
- Click OK to copy the sheet.
- The named formulas are now in the destination workbook.
- If desired, delete the copied sheet. The named formulas will remain.
- What is the 4% retirement rule?
- How the 4% rule works
- What we need to model in Excel
- The model in Excel
- Traditional approach (Sheet1)
- Hybrid approach (Sheet2)
- Single formula approach (Sheet3)
- Summary and conclusion
- Functions used in the workbook
- Instructions
What is the 4% retirement rule?
If you look into retirement planning, you’ll probably run into the 4% retirement rule, one of the most well-known (and frequently cited) guidelines for retirement spending. In brief, the 4% retirement rule tries to answer this question in a simple way: “How much can I safely withdraw from my retirement savings each year without running out of money?” The answer? About 4%, adjusted for inflation.
The rule came out of research conducted by a financial advisor named Bill Bengen in 1994. His goal was to determine a safe withdrawal rate (SAFEMAX) that would allow retirees to maintain their standard of living throughout a 30-year retirement without running out of money, even across periods of poor market performance and high inflation.
Based on a historical reconstruction of retiree portfolios since 1926, Bengen recommended a 4% withdrawal rate for the first year, followed by cost-of-living adjustments each succeeding year. Although Bengen himself didn’t refer to a “4% rule” (and later changed his recommendation to 4.5% and then to 4.7%), the name stuck and carries on to this day.
How the 4% rule works
Applying the rule is simple: in your first year of retirement, you withdraw 4% of your total portfolio balance. In each subsequent year, you adjust that initial dollar amount for inflation rather than recalculating 4% of your current balance. For example, if you retire with a $1 million portfolio, you would withdraw $40,000 in year one. If inflation is 3% that year, you’d withdraw $41,200 in year two, and so on. The idea is to provide predictable, inflation-adjusted income while preserving the portfolio across various market conditions across the entire retirement period.
For those planning retirement, the 4% rule serves as both a withdrawal strategy and a savings target. If you know your desired annual retirement income, you can work backward to determine how much you need to save: simply multiply your target income by 25 (since 4% × 25 = 100%). While the rule has plenty of critics and may need adjustment based on individual circumstances, it remains a useful starting point for retirement planning. It is also a great example of a problem that can be modeled in Excel, where you can easily test various scenarios and assumptions.
I’m not a financial advisor. My goal is not to convince you that the 4% rule is the best way to plan for retirement. My goal is to show how you can model a problem like this in Excel in different ways.
What we need to model in Excel
Before we get into details, let’s review what we need to model: Beginning with a given starting balance (total retirement savings), we need to calculate 4% of the starting balance, then adjust the withdrawal for inflation annually, add in growth and show how this plays out over 30 years. We’ll want inputs for starting balance, withdrawal rate, growth rate, inflation rate, age at retirement, and the number of years in retirement, so that we can fiddle with these numbers to see how they impact the final outcome:
| Input | Description | Example value |
|---|---|---|
| Starting balance | Total retirement savings at the beginning | $1,000,000 |
| Withdrawal rate | Initial withdrawal percentage | 4% |
| Annual growth rate | Expected portfolio return | 7% |
| Inflation rate | Annual cost-of-living increase | 2.5% |
| Age at retirement | Starting age | 65 |
| Years in retirement | Duration of withdrawal period | 30 |
In our Excel model, we’ll use constant rates for both growth and inflation throughout the entire retirement period. This is a simplification that makes the model easier to build and understand. In reality, portfolio returns vary significantly from year to year (i.e. gains of 20% on year, others losses of 15% in another) and you would adjust withdrawals based on actual annual inflation rather than an assumed rate. The sequence of these returns matters a lot: poor market performance early in retirement is far more damaging than the same poor returns later on. This is called “sequence of returns risk,” and it’s why Bengen tested his 4% rule against historical market data, including worst-case scenarios like retiring in 1968 just before a major market decline and high inflation period. Our constant-rate model won’t capture this real-world volatility, but it will demonstrate the mechanics of how the 4% rule works.
Using the inputs above, we need to generate a “withdrawal schedule” that shows how the portfolio changes over a period of 30 years. Once we have the schedule in place, we can calculate the total withdrawals and a final balance to see if the portfolio survived retirement. We also want to calculate a “real value” of the ending balance, adjusted for inflation. Finally, we want the withdrawal schedule to be dynamic, so that it expands or contracts as needed when the number of years in retirement changes. The screenshot below shows the basic idea. Note the key inputs are in the range C5:C10. These are the variables that control the outputs. The outputs are summarized in the range F5:F9. The withdrawal schedule begins in row 13 and covers 30 years.
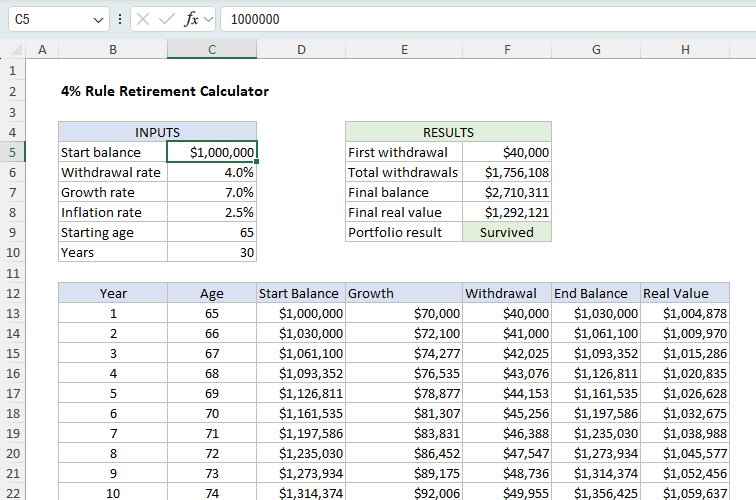
The model in Excel
Of course, there are different ways to model a problem like this in Excel, especially since Excel now supports dynamic array formulas , which offer entirely new ways to approach multi-row calculations. The attached workbook explores three different ways to model the 4% retirement rule. All approaches use the same inputs and produce identical outputs, but they build the withdrawal schedule in progressively more advanced ways — from classic formulas to modern dynamic arrays.
- Sheet1 - Traditional approach - Classic row-by-row formulas with relative and absolute references.
- Sheet2 - Hybrid approach - One dynamic array formula per column.
- Sheet3 - Single formula approach - One formula generates the entire table.
The workbook also has a fourth sheet with simple instructions on how to use the workbook.
The point of this exercise is not to convince you that one approach is better than the other. The point is to look at different ways to model a problem like this in Excel, and explore some of the pros and cons of each approach. Let’s start with the traditional approach.
As shipped, all three worksheets have the same inputs and produce the same outputs. The only difference is the approach used to build the withdrawal schedule and the summary results in column F. On any sheet, you can modify the inputs in the range C5:C10 to see how the outputs change. The changes you make on one sheet will not affect the other sheets.
Traditional formula approach (Sheet1)
This worksheet uses a classic row-by-row setup — each row represents one year of retirement, and every column holds a key variable: Year, Age, Start Balance, Growth, Withdrawal, End Balance, and Real Value (inflation-adjusted balance). Formulas are copied down and use a mix of relative and absolute references so that each row refers correctly to the previous year’s results. It takes more than 200 formulas to build the entire withdrawal schedule for 30 years.
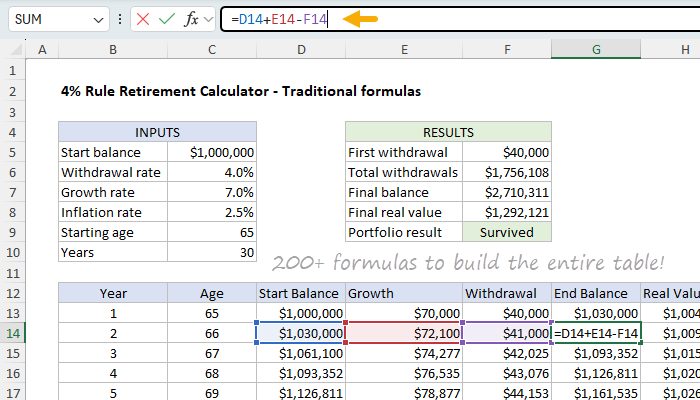
Here is how the formulas are set up:
| Column | Description | Example formula (first data row) |
|---|---|---|
| B - Year | Sequence of years | 1 in row 13, then B13+1 |
| C - Age | Age in each year | =C9 in row 13, then C13+1 |
| D - Start Balance | Beginning portfolio value | =C5 in row 13, then G13 |
| E - Growth | Portfolio growth | =D13*$C$7 |
| F - Withdrawal | Inflation-adjusted withdrawal | =C5C6 in row 13, then =F13(1+$C$8) |
| G - End Balance | End of year balance | =D13+E13-F13 |
| H - Real Value | Inflation-adjusted end balance | =PV($C$8,B13,0,-G13) |
The summary results in the range F5:F9 are generated with the following formulas:
| Cell | Description | Formula |
|---|---|---|
| F5 | First withdrawal | =C5*C6 |
| F6 | Total withdrawals | =SUM(F13:F100) |
| F7 | Final balance | =LOOKUP(2,1/(G13:G100<>””),G13:G100) |
| F8 | Total real value | =LOOKUP(2,1/(H13:H100<>””),H13:H100) |
| F9 | Portfolio result | =IF(F7>0,“Survived”,“Depleted”) |
The LOOKUP function is used to find the last non-empty cell in the range G13:G100 and H13:H100. These ranges are oversized to allow the table to be extended if needed. For more details on this formula see Get value of last non-empty cell . The LOOKUP function works in all Excel versions. You could use the same trick to pull the last year in column B into C10 (Years) if you like, but I have left it as a static value to avoid confusion. For more information on the PV function, see PV function .
Note that a key feature of this approach is that formulas in row 1 of the schedule are often different from the formulas in the subsequent rows. These formulas must be carefully crafted to ensure that they reference the correct cells, which involves using a mix of relative and absolute references. It also means a user must be careful if changes are made to the withdrawal schedule. On the other hand, this approach is easy to understand and audit, and works in all Excel versions.
Pros and cons
| Pros | Cons |
|---|---|
| Easy to understand and audit | Must copy or extend formulas manually |
| Works in all Excel versions | Fixed size, table is not dynamic |
| Great for teaching relative/absolute references | Prone to reference errors if rows are inserted or deleted |
Hybrid formula approach (Sheet2)
This sheet uses dynamic array formulas to generate each full column of data automatically. Every column uses one formula that spills to the required number of rows, tied initially to the Years (C10) input. It takes 7 formulas to build the entire withdrawal schedule, one per column:
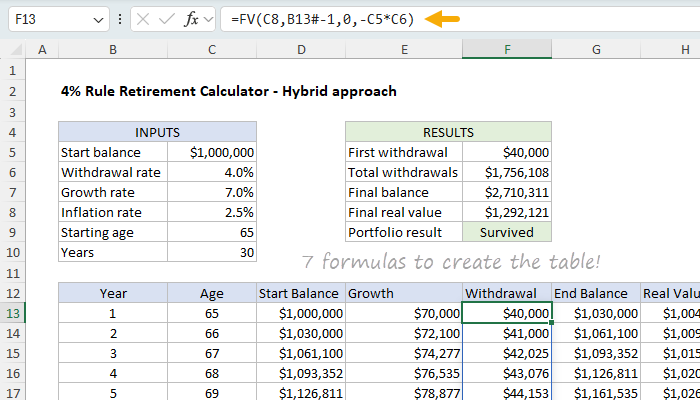
The formulas are set up like this:
| Column | Description | Formula |
|---|---|---|
| B - Year | Sequence of years | =SEQUENCE(C10) |
| C - Age | Starting age + sequence | =SEQUENCE(C10,1,C9) |
| D - Start Balance | Prior year’s end | =VSTACK(C5,DROP(G13#,-1)) |
| E - Growth | Annual growth | =D13#*C7 |
| F - Withdrawal | Inflation-adjusted withdrawal | =FV(C8,B13#-1,0,-C5*C6) |
| G - End Balance | Balance after growth and withdrawal | =SCAN(C5,F13#,LAMBDA(bal,wd,bal*(1+C7)-wd)) |
| H - Real Value | Inflation-adjusted balance | =PV(C8,B13#,0,-G13#) |
The summary results in the range F5:F9 are generated with the following formulas:
| Cell | Description | Formula |
|---|---|---|
| F5 | First withdrawal | =C5*C6 |
| F6 | Total withdrawals | =SUM(F13#) |
| F7 | Final balance | =TAKE(G13#,-1) |
| F8 | Total real value | =TAKE(H13#,-1) |
| F9 | Portfolio result | =IF(F7>0,“Survived”,“Depleted”) |
This approach in Sheet2 is a great example of how formulas can be anchored to an existing spill range so that columns automatically expand or contract as needed. All the formulas in columns D through H are anchored to a spill range for years that begins in cell B13, so that they automatically adjust to the correct number of rows as needed. The spill range for years is generated with the SEQUENCE function like this:
=SEQUENCE(C10) // generate years 1 to 30
If the number of years in cell C10 is changed, the rows in the Year column will expand or contract as needed. Column C (Age) is also created with the SEQUENCE function, which is configured to generate a sequence of ages that spans the same number of years as the Year column, beginning at the starting age in cell C9, and increasing by 1 for each year.
=SEQUENCE(C10,1,C9) // generate ages 65 to 94
Column D (Start Balance) is generated with a clever combination of the DROP and VSTACK functions, like this:
=VSTACK(C5,DROP(G13#,-1))
DROP removes the last (unused) year-end balance from the spill range in column G (End Balance). VSTACK then inserts the starting balance in C5 at the top of the list and appends the year-end balance. It is a bit confusing that the start balance comes before the end balance, and yet the start balance depends on the end balance. But it makes sense if you think about it - the start balance is really the same as the end balance shifted down by one year. In other words, we need the end balance to know the starting balance in the next year.
Column E (Growth) is generated by multiplying the start balance by the growth rate:
=D13#*C7
Column F (Withdrawal) is generated by the FV function . The FV function calculates the future value of an investment based on an initial principal balance, a fixed annual interest rate, the number of compounding periods, and the periodic payment. In this case, we are using the FV function to calculate the future value of the initial withdrawal amount, adjusted for inflation, over the number of years in the withdrawal schedule. The formula looks like this:
=FV(C8,B13#-1,0,-C5*C6)
The rate is supplied as the inflation rate in C8 (2.5%), the number of periods is the number of years in the withdrawal schedule minus 1 B13#-1 , the present value is the starting balance multiplied by the withdrawal rate -C5*C6 , and the payment is 0 since there are no periodic payments.
We use the FV function here to calculate an inflation-adjusted withdrawal, but we could use the equivalent long-hand formula: =C5C6(1+C8)^(B13#-1) . Both formulas will return the same result.
Column G (End Balance) is generated by the SCAN function . The SCAN function applies a LAMBDA function to a series of values and accumulates the results. In this case, we are using the SCAN function to calculate the year-end balances by applying the LAMBDA function to the starting balance and the withdrawal. The formula looks like this:
=SCAN(C5,F13#,LAMBDA(bal,wd,bal*(1+C7)-wd))
The starting balance is supplied as the starting value in C5 , the series of values is the series of withdrawals in F13# , and the LAMBDA function is LAMBDA(bal,wd,bal*(1+C7)-wd) . The LAMBDA function is applied to the starting value and the first value in the series, and the result is returned. The result is then used as the starting value for the next iteration of the LAMBDA function. This process is repeated for each value in the series. With 30 years in C10, the result is a series of 30 year-end balances.
Column H (Real Value) is generated by the PV function . The PV function calculates the present value of an investment based on a future value, a fixed annual interest rate, the number of compounding periods, and the periodic payment. In this case, we are using the PV function to calculate the present value of the year-end balances, adjusted for inflation. The formula looks like this:
=PV(C8,B13#,0,-G13#)
The rate is supplied as the inflation rate in C8 (2.5%), the number of periods is the number of years in the withdrawal schedule B13# , the future value is the year-end balances in G13# , and the payment is 0 since there are no periodic payments.
We use the PV function here to calculate an inflation-adjusted end balance, but we could use the equivalent long-hand formula: =G13#/(1+$C$8)^(B13#) . Both formulas will return the same result.
As mentioned above, because these formulas are tied to the spill ranges, beginning with the spill range in column B (Year), all columns will resize as needed if the number of years in retirement C10 is changed.
Excel’s PV and FV functions use a cash flow convention where you negate values that represent outflows. This is why the present value is negative in the FV function and the future value is positive in the PV function. The negative sign ensures that we get a positive result.
Pros and cons
| Pros | Cons |
|---|---|
| Fully dynamic — table resizes automatically | Requires Excel 365 |
| One formula per column, no locked references | Depends on anchoring to spill ranges |
| Clean, scalable, and easy to read | New functions like SCAN and VSTACK may be unfamiliar |
| Fewer formulas to manage | More abstract than row-by-row approach |
Single formula approach (Sheet3)
In this sheet, the entire withdrawal schedule is generated by a single dynamic array formula that combines LET, SEQUENCE, FV, SCAN, VSTACK, and HSTACK. Each variable is defined and reused inside a single expression, which spills into a complete table. It takes 9 formulas to build the entire withdrawal schedule:
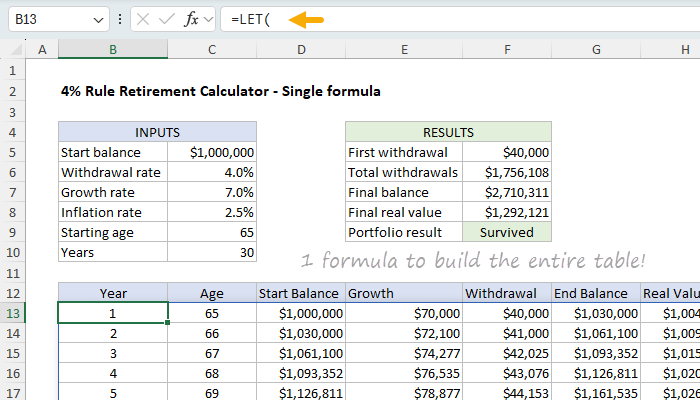
The formula in B13 looks like this:
=LET(
start,C5, wr,C6, gr,C7, ir,C8, age,C9, n,C10,
yrs,SEQUENCE(n),
ages,SEQUENCE(n,1,age),
wds,FV(ir,yrs-1,0,-start*wr),
ends,SCAN(start, wds, LAMBDA(bal,wd, bal*(1+gr)-wd)),
starts,VSTACK(start,DROP(ends,-1)),
growth,starts*gr,
real,PV(ir,yrs,0,-ends),
HSTACK(yrs,ages,starts,growth,wds,ends,real)
)
This formula uses the LET function to define a series of variables that are used to generate the withdrawal schedule:
| Variable | Description |
|---|---|
| start | Starting portfolio balance from C5 ($1,000,000) |
| wr | Withdrawal rate from C6 (4%) |
| gr | Annual growth rate from C7 (7%) |
| ir | Inflation rate from C8 (2.5%) |
| age | Starting age from C9 (65) |
| n | Number of years from C10 (30) |
| yrs | Sequence of years 1 to n |
| ages | Sequence of ages starting at age |
| wds | Annual withdrawals, adjusted for inflation via FV function |
| ends | Year-end balances generated by SCAN |
| starts | Start balances built from prior year’s end |
| growth | Annual growth amounts from start balance * growth rate |
| real | Inflation-adjusted end balances via PV function |
The summary results in the range F5:F9 are generated with the following formulas:
| Cell | Description | Formula |
|---|---|---|
| F5 | First withdrawal | =C5*C6 |
| F6 | Total withdrawals | =SUM(CHOOSECOLS(B13#,5)) |
| F7 | Final balance | =TAKE(CHOOSECOLS(B13#,6),-1) |
| F8 | Total real value | =TAKE(CHOOSECOLS(B13#,7),-1) |
| F9 | Portfolio result | =IF(F7>0,“Survived”,“Depleted”) |
This is clearly the most complex formula of the three approaches, but it is also the most compact and efficient. One nice feature of building the formula this way is that once the variables are defined, they can be used directly in other parts of the formula instead of cell references, making the formula easier to read and understand. Briefly, the formula works like this:
- Define the starting balance (start), withdrawal rate (wr), growth rate (gr), inflation rate (ir), starting age (age), and number of years (n). start,C5, wr,C6, gr,C7, ir,C8, age,C9, n,C10
- Generate a sequence of years (yrs) from 1 to n. yrs,SEQUENCE(n)
- Generate a sequence of ages (ages) starting at the starting age. ages,SEQUENCE(n,1,age)
- Generate a series of annual withdrawals (wds), adjusted for inflation via the FV function . wds,FV(ir,yrs-1,0,-start*wr)
- Generate a series of year-end balances (ends) by applying the SCAN function to the starting balance and the series of annual withdrawals. ends,SCAN(start, wds, LAMBDA(bal,wd, bal*(1+gr)-wd))
- Generate a series of start balances (starts) by building from the prior year’s end. starts,VSTACK(start,DROP(ends,-1))
- Generate a series of annual growth amounts (growth) by multiplying the start balance by the growth rate. growth,starts*gr
- Generate a series of inflation-adjusted end balances (real) by applying the PV function to the year-end balances. real,PV(ir,yrs,0,-ends)
- Combine all the series into a single table using the HSTACK function. HSTACK(yrs,ages,starts,growth,wds,ends,real)
For details on the functions used in the formula, see the Functions used in the workbook section below.
Pros and cons
| Pros | Cons |
|---|---|
| One formula builds the entire table | Advanced Excel skills required |
| Fully dynamic, no fixed ranges | Requires Excel 365 |
| Compact and efficient | Steeper learning curve |
| Single source of truth | Harder to audit cell-by-cell |
Summary and conclusion
All three worksheets produce the same result: a year-by-year simulation of the 4% retirement rule . The difference lies in how the withdrawal schedule is built.
- Traditional (Sheet1) builds the table step-by-step using relative and absolute references.
- Hybrid (Sheet2) constructs each column with a single dynamic array formula.
- Single (Sheet3) uses one dynamic array formula to generate the entire table.
Each approach is valid — your choice depends on your priorities for transparency and flexibility, and your comfort level with modern Excel features. Which approach do you like best?
| Approach | Strengths | Limitations | Best use case |
|---|---|---|---|
| Traditional | Simple, visual, easy to follow | Manual setup, not dynamic | Teaching, compatibility with older Excel |
| Hybrid | Dynamic arrays, clear logic, no locked references | Requires Excel 365 | Modern Excel modeling, learning SCAN and VSTACK |
| Single | Fully dynamic, one formula, easy to reuse | Harder to audit visually | Reusable templates, LAMBDA functions, advanced modeling |
Functions used in the workbook
The models in the attached workbook use many Excel functions, some of which you might not be familiar with. Below is a list of the functions used, with links to pages with more details and examples. If you are new to dynamic array formulas, you might also want to check out this article: Dynamic array formulas in Excel .
| Function | Description |
|---|---|
| CHOOSECOLS | Extracts specific columns from an array |
| DROP | Removes rows or columns from the beginning or end of an array |
| FV | Calculates the future value of an investment |
| HSTACK | Combines arrays horizontally (side by side) |
| IF | Returns one value if a condition is true, another if false |
| LAMBDA | Creates custom functions using Excel’s formula language |
| LET | Assigns names to calculation results for use in formulas |
| PV | Calculates the present value of an investment |
| SCAN | Applies a function to each element in an array and returns intermediate results |
| SEQUENCE | Generates a sequence of numbers |
| SUM | Adds numbers in a range or array |
| TAKE | Returns a specified number of rows or columns from an array |
| VSTACK | Combines arrays vertically (stacked on top of each other) |
Instructions
As shipped, all three worksheets have the same inputs and produce the same outputs. The only difference is the approach used to build the withdrawal schedule. On any sheet, you can modify the inputs in the range C5:C10 to see how the outputs change. The changes you make on one sheet will not affect the other sheets. For example, if you change the starting balance in C5 on Sheet1 from $1,000,000 to $1,500,000, the starting balance in the other two sheets will not change.
- Click through the 3 worksheets to see how the withdrawal schedule is built.
- Modify the input cells in column C to test different scenarios.
- Watch how the projection table updates automatically.
- Pay attention to the Final Balance in E7 — does it go negative?
- Compare Real Value to see inflation’s impact on purchasing power.
Notes
While my Excel model uses constant growth and inflation rates for simplicity, Bengen’s original research was far more rigorous. He used actual historical data from 1926 onward, testing over 50 different 30-year retirement periods with the real year-by-year stock returns, bond returns, and inflation rates. This included the Great Depression, the 1970s stagflation, bull markets, bear markets, and everything in between. Bengen tested multiple portfolio allocations ranging from 0% to 100% stocks, focusing primarily on 50/50 and 75/25 stock-to-bond splits. The 4% withdrawal rate emerged because it was the maximum rate that survived even the worst historical scenario (retiring late in 1968). The beauty of his approach was testing against actual market sequences, not constant averages.
- The 4% rule assumes a roughly 60/40 stock-bond portfolio.
- The historical success rate is very high over 30-year periods.
- Sequence-of-returns risk and market timing are not modeled in this workbook.
- Other income sources, such as Social Security, are not considered.
- Taxes, healthcare costs, and longevity are not part of this model.
Further reading
- How Much Is Enough? - Bill Bengen on FA Magazine
- How the 4% Rule Works - Rob Berger
- Bill Bengen’s Latest Insights on the 4% Rule