Purpose
Return value
Syntax
=SIN(number)
- number - The angle in radians for which you want the sine.
Using the SIN function
The SIN function returns the sine of an angle provided in radians. In geometric terms, the sine of an angle returns the ratio of a right triangle’s opposite side over its hypotenuse. For example, the sine of PI()/6 radians (30°) returns the ratio 0.5.
=SIN(PI()/6) // Returns 0.5
Using Degrees
To supply an angle to SIN in degrees, multiply the angle by PI()/180 or use the RADIANS function to convert to radians. For example, to get the SIN of 30 degrees, you can use either formula below:
=SIN(30*PI()/180)
=SIN(RADIANS(30))
Explanation
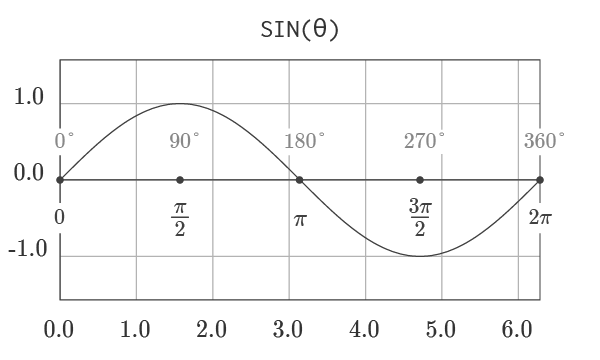
The graph of sine, shown above, visualizes the output of the function for all angles from 0 to a full rotation. The function is periodic, so after a full rotation, the output of the function repeats. Geometrically, the function returns the y -component of the point corresponding to an angle on the unit circle. The function’s output will always be in the range [-1, 1].
Graph courtesy of wumbo.net .
Purpose
Return value
Syntax
=SINH(number)
- number - The hyperbolic angle.
Using the SINH function
The SINH function returns the hyperbolic sine of a number. Given the input 1, the function returns the value 1.175201194.
=SINH(0) // returns 1.175201194
Explanation
The hyperbolic sine function returns the vertical component of the point on the right branch (x ≥ 1) of the unit hyperbola corresponding to the hyperbolic angle given as input.

Together with hyperbolic cosine , the functions parameterize the right branch of the unit hyperbola given by the equation x² - y² = 1. In plain language, this means that the two functions trace out the shape of the right branch of the unit hyperbola.
Given a hyperbolic angle corresponding to a point on the hyperbola’s curve, SINH returns the vertical component of the point, while COSH returns the horizontal component of the point. For example, given the hyperbolic angle -1, hyperbolic cosine returns the x-component 1.543080635, and hyperbolic sine returns the y-component -1.175201194.

Here is a table that shows some points on the unit hyperbola formed by COSH and SINH.

As the hyperbolic angle increases positively, the vertical component goes to infinity, and as the hyperbolic angle increases negatively, the vertical component goes to negative infinity. This is different from the sine function , which is periodic and repeats values.

Images courtesy of wumbo.net .