Explanation
The SQRT function is fully automatic and will return the square root of any positive number. For example, to get the square root of 25, you can use:
=SQRT(25) // returns 5
To get the square root of 16:
=SQRT(16) // returns 4
To get the square root of a number in cell A1:
=SQRT(A1) // square root of A1
Negative numbers
If you give SQRT a negative number, it returns a #NUM! error:
=SQRT(-4) // returns #NUM!
To use the SQRT function with negative numbers you nest the ABS function inside SQRT like this:
=SQRT(ABS(-4)) // returns 2
The ABS function converts the negative number to a positive number and returns the result to the SQRT function, which calculates a final result.
Exponent operator (^)
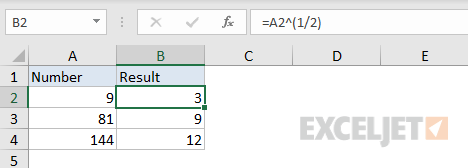
Another way to get the square root of a number in Excel is to use the exponent operator , the caret (^). To return the square root of a number in A1, you can use a formula like this:
=A1^(1/2) // square root
The screen below shows how this formula looks in a worksheet:
Nth root
Excel does not have a built-in function to get the nth root of a number. However, you can calculate the nth root of a number by raising the number to the power of 1/n:
=A1^(1/n) // nth root
The screen below shows this formula in use:

Square root with POWER
You can get also get the square root or nth root of a number with the POWER function . POWER is a general function for raising a number to a given power, for example:
=POWER(2,2) // returns 4
=POWER(2,3) // returns 8
=POWER(2,4) // returns 16
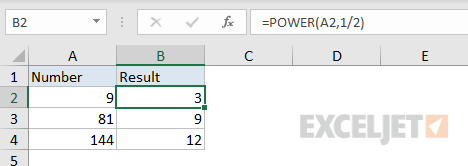
The general form for getting the nth root with POWER is:
=POWER(A1,1/n) // nth root
For example:
=POWER(A1,1/2) // square root
=POWER(A1,1/3) // cube root
=POWER(A1,1/4) // fourth root
The screen below shows how the POWER function can be used to calculate square root of the numbers in column A:
Explanation
Standard deviation in Excel
Standard deviation is a measure of how much variance there is in a set of numbers compared to the average (mean) of the numbers. To calculate standard deviation in Excel, you can use one of two primary functions, depending on the data set. If the data represents the entire population, you can use the STDEV.P function . IF the data is just a sample, and you want to extrapolate to the entire population, you can use the STDEV.S function to correct for sample bias as explained below. Both functions are fully automatic.
Bessel’s correction, STDEV.P vs. STDEV.S
When you calculate statistics for an entire population (mean, variance, etc.) results are accurate because all data is available. However, when you calculate statistics for a sample, results are estimates and therefore not as accurate.
Bessel’s correction is an adjustment made to correct for bias that occurs when working with sample data. It appears in formulas as n-1, where n is the count. When working with a sample population, Bessel’s correction can provide a better estimation of the standard deviation. In the context of Excel and standard deviation, the key thing to understand is:
- The STDEV.S function uses Bessel’s correction
- The STDEV.P function does not
When should you use STDEV.S, which includes Bessel’s correction? It depends.
- If you have data for an entire population, use STDEV.P
- If you have an appropriately large sample and you want to approximate standard deviation for the entire population, use the STDEV.S function.
- If you have sample data, and only want standard deviation for the sample, without extrapolating for the entire population, use the STDEV.P function.
Remember that a small sample is not likely to be a good approximation of a population in most cases. On the other hand, a large enough sample size will approach the statistics produced for a population. In these cases, Bessel’s correction may not be useful.
Manual calculations for standard deviation
The screen below shows how to manually calculate standard deviation in Excel.

Column D calculates Deviation, which the value minus mean. The formula in D5, copied down is:
=C5-AVERAGE($C$5:$C$14)
Column E shows deviations squared. The formula in E5, copied down is:
=(D5)^2
In H5 we calculate standard deviation for the population with this formula:
=SQRT(SUM(E5:E14)/COUNT(E5:E14))
In H6 we calculate standard deviation for a sample with a formula that uses Bessel’s correction:
=SQRT(SUM(E5:E14)/(COUNT(E5:E14)-1))
Older functions
You may notice that Excel contains older functions, STDEVP and STDEV which also calculate standard deviation. In short:
- STDEV.P replaces the STDEVP function, with identical behavior.
- STDEV.S replaces the STDEV function, with identical behavior.
Although STDEVP and STDEV still exist for backwards compatibility, Microsoft recommends that people use the newer STDEV.P and STDEV.S functions instead.